Word Embedding Analogies: Understanding King - Man + Woman = Queen
A surprising property of word vectors is that word analogies can often be solved with vector arithmetic. Most famously,
\[\vec{king} - \vec{man} + \vec{woman} \approx \vec{queen}\]But why? Why do arithmetic operators apply to vectors generated by non-linear models such as word2vec? What conditions have to be satisfied by the training corpus for these analogies to hold in the vector space?
There have been surprisingly few theories trying to explain this phenomenon. Those that do exist, including the latent variable model1 (Arora et al., 2016) and the paraphrase model2 (Gittens et al., 2017; Allen and Hospedales, 2019) make strong assumptions about the embedding space or distribution of word frequencies. There is no empirical evidence to support these theories either.
In our ACL 2019 paper, “Towards Understanding Linear Word Analogies”, we provide a formal explanation of word analogy arithmetic for GloVe and skipgram with negative sampling (SGNS) without making such strong assumptions. In turn, our theory provides:
- the first information theoretic interpretation of Euclidean distance in SGNS and GloVe spaces
- novel justification for using addition to compose SGNS word vectors
- a formal proof of the intuitive explanation of word analogies, proposed in the GloVe paper
Most importantly, our theory is also supported by empirical evidence, making it much more tenable than past explanations.
The Structure of Word Analogies
In the broadest sense, a word analogy is a statement of the form “a is to b as x is to y”, which asserts that a and x can be transformed in the same way to get b and y, and vice-versa. Given that this is just an invertible transformation, we can state it more formally:
A word analogy $f$ is an invertible transformation that holds over a set of ordered pairs $S$ iff $\forall\ (x,y) \in S, f(x) = y \wedge f^{−1}(y) = x$. When $f$ is of the form $\vec{x} \mapsto \vec{x} + \vec{r}$, it is a linear word analogy.
These linear word analogies, such as $\vec{king} + (\vec{woman} - \vec{man}) \approx \vec{queen}$, are what we’d like to explain. When they hold exactly, they form a parallelogram structure in the vector space (by definition):
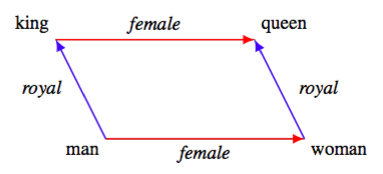
Parallelograms have several useful properties that we can exploit. For one, a quadrilateral is a parallelogram iff each pair of opposite sides is equal in length (and in higher-dimensional spaces, all four points are coplanar). This means that
A linear word analogy holds exactly over a set of ordered word pairs $S$ iff $ \| \vec{x} - \vec{y} \|^2 $ is the same for every word pair, $ \| \vec{a} - \vec{x} \|^2 = \| \vec{b} - \vec{y} \|^2 $ for any two word pairs, and the vectors of all words in $S$ are coplanar.
Interpreting Inner Products
In order to meaningfully interpret the conditions above, we need to be able to interpret the inner product (i.e., the dot product) of two word vectors.
However, the literature only tells us how to interpret the inner product of a word and context vector. Recall that SGNS and GloVe create two representations for each word – one for when it is the target word and one for when it is a context word (i.e., in the context window of some other word). The latter representation, called the context vector, is typically discarded after training.
We can interpret the inner product of a word and context vector because even though SGNS and GloVe learn vectors iteratively in practice, they are implicitly factorizing a word-context matrix containing a co-occurrence statistic. When the factorized matrix can be perfectly reconstructed, where $\vec{x}, \vec{y}$ are word vectors and $\vec{x}_c, \vec{y}_c$ their corresponding context vectors:
\[\text{GloVe}: \langle \vec{x}, \vec{y}_c \rangle = \log X_{x,y} - b_x - b_y\] \[\text{SGNS}: \langle \vec{x}, \vec{y}_c \rangle = \text{PMI}(x,y) - \log k\]The first identity is the local objective of GloVe, where $X_{x,y}$ denotes the co-occurrence count and $b_x, b_y$ denote the learned biases for each word. The second identity is from Levy and Goldberg (2014), who showed that SGNS is implicitly factorizing the pointwise mutual information (PMI) matrix of the word-context pairs shifted by log $k$, the number of negative examples. Since the matrix being factorized is symmetric, $\langle \vec{x}, \vec{y}_c \rangle = \langle \vec{x}_c, \vec{y} \rangle$.
Using these identities and the symmetry of the factorized word-context matrix, we prove that any linear analogy $f$ that holds in the word space has a corresponding linear analogy $g$ that holds in the context space. More specifically:
A linear analogy $f : \vec{x} \mapsto \vec{x} + \vec{r}$ holds over ordered pairs $S$ in an SGNS or GloVe word space with no reconstruction error iff $\exists\ \lambda \in \mathbb{R}, g: \vec{x}_c \mapsto \vec{x}_c + \lambda \vec{r}$ holds over $S$ in the corresponding context space.
This theoretical finding concurs with prior empirical and theoretical work. Most work often assumes $\lambda \approx 1$ in practice, which we find to be true as well. This finding allows us to write $ \| \vec{x} - \vec{y} \|^2 $ as the inner product of $\vec{x} - \vec{y}$ and $\vec{x}_c - \vec{y}_c$ scaled by $1/\lambda$, making it much more interpretable.
When do Linear Word Analogies Hold?
We now know the conditions that need to be satisfied for a linear analogy to hold exactly in vector space and how to interpret the inner product of two word vectors.
This means that we can now use the SGNS or GloVe identity above to rewrite these conditions in terms of statistics over the training corpus. Regardless of which identity we choose, we arrive at the Co-occurrence Shifted PMI Theorem (or csPMI Theorem, for short). Remarkably, even though SGNS and GloVe are completely different embedding models, the conditions under which analogies manifest in their vector spaces is the same!
Co-occurrence Shifted PMI Theorem
Let $\text{csPMI}(x,y) = \text{PMI}(x,y) + \log p(x,y)$, $W$ be an SGNS or GloVe word vector space with no reconstruction error, $M$ be the word-context matrix that is implicitly factorized by SGNS or GloVe, and $S$ be a set of ordered pairs such that $|S| > 1$ and all words in $S$ have a vector in $W$.
A linear analogy $f$ holds over word pairs $S$ iff
- $\text{csPMI}(x,y)$ is the same for every word pair $(x,y)$
- $\text{csPMI}(a, x) = \text{csPMI}(b, y)$ for any two word pairs $(x, y), (a, b)$
- $\{ M_{a,\cdot} - M_{y,\cdot}$, $M_{b,\cdot} - M_{y,\cdot}$, $M_{x,\cdot} - M_{y,\cdot} \}$ are linearly dependent for any two word pairs
For example, for $\vec{king} - \vec{man} + \vec{woman} = \vec{queen}$ to hold exactly in a noiseless SGNS or GloVe space, we would need the following to be satisfied by the training corpus3:
- csPMI(king, queen) = csPMI(man, woman)
- csPMI(king, man) = csPMI(queen, woman)
- row vectors of the four words in the factorized word-context matrix to be coplanar
Robustness to Noise
Note that the conditions above need to be satisfied for an analogy to hold exactly in a noiseless space. In practice, however, these conditions are rarely satisfied perfectly and linear word analogies do not hold exactly.
Yet they are said to exist anyway – why?
-
The definition of vector equality is looser in practice. An analogy task (a,?)::(x,y) is solved by finding the word closest to $\vec{a} + \vec{y} - \vec{x}$ (excluding $\vec{a}, \vec{x}, \vec{y}$ as possible answers). The correct answer can be found even when it is not exact and does not lie on the plane defined by $\vec{a}, \vec{x}, \vec{y}$.
-
Although the theorem assumes no reconstruction error for all word pairs, if we ignore the coplanarity constraint, only $|S|^2+2|S|$ pairs need to be recovered for $f$ to hold exactly over $S$.
-
Analogies mostly hold over frequent word pairs, which are associated with less noise. For example, analogies of countries and their capitals, which have a median frequency of 3436.5 in Wikipedia, can be solved with 95.4% accuracy; analogies of countries and their currency, which have a median frequency of just 19, can only be solved with 9.2% accuracy.4
Implications
The Intuition was Right all Along
The original GloVe paper conjectured that an analogy of the form “a is to b as x is to y” holds iff for every word $w$ in the vocabulary,
\[\frac{p(w|a)}{p(w|b)} \approx \frac{p(w|x)}{p(w|y)}\]This has long been considered the intuitive explanation of word analogies, despite lacking a formal proof. In our paper, we show that this conjecture is indeed true (at least for SGNS).
Vector Addition as an Analogy
By introducing the idea of a null word $\emptyset$, which maps to the zero vector in any space, we can frame vector addition ($\vec{x} + \vec{y} = \vec{z}$) as a linear analogy over $ \{(x,z), (\emptyset, y)\} $. If $z$ were in the vocabulary, $\text{csPMI}(x,z) = \log p(y) + \delta$, where $\delta \in \mathbb{R}$ is a model-specific constant. This, in turn, implies that
\[p(x) > p(y) \iff \text{csPMI}(z,y) > \text{csPMI}(z,x)\]This suggests that the addition of two SGNS vectors implicitly downweights the more frequent word, as weighting schemes (e.g., SIF, TF-IDF) do ad hoc. For example, if the vectors for $x =$ ‘the’ and $y =$ ‘apple’ were added to create a vector for $z =$ ‘the_apple’, and if this were actually a term in the vocabulary, we’d expect csPMI(‘the_apple’, ‘apple’) > csPMI(‘the_apple’, ‘the’). Although, in reality, most bigrams are not terms in the vocabulary, this helps explain empirical observations that averaging word vectors is a surprisingly effective way of composing them.
Interpreting Euclidean Distance
$\exists\ \lambda \in \mathbb{R}^+, \alpha \in \mathbb{R}^-$ such that for any two words $x, y$ in a noiseless SGNS or GloVe space,
\[\lambda \| \vec{x} - \vec{y} \|^2 = - \text{csPMI}(x,y) + \alpha\]The squared Euclidean distance between two words is simply a decreasing linear function of their csPMI. This is intuitive: the more similar two words are in the training corpus – as measured by the csPMI – the smaller the distance between their vectors. Still, to our knowledge, this is the first information theoretic interpretation of Euclidean distance in word vector spaces.
Empirical Evidence
As mentioned earlier, a key problem with prior theories is that there is very little (if any) empirical evidence supporting them. Below, we present two empirical findings that lend credence to ours.
Estimating csPMI
According to the csPMI Theorem, if an analogy holds exactly over a set of word pairs in a noiseless word vector space, then each pair has the same csPMI value. To test this, we count word co-occurrences in Wikipedia and calculate the mean csPMI values for analogies in the word2vec paper over the word pairs for which they should hold (e.g., {(Paris, France), (Berlin, Germany)} for capital-world). We then try to solve these analogies – in the traditional manner, by minimizing cosine distance – using SGNS vectors trained on Wikipedia.
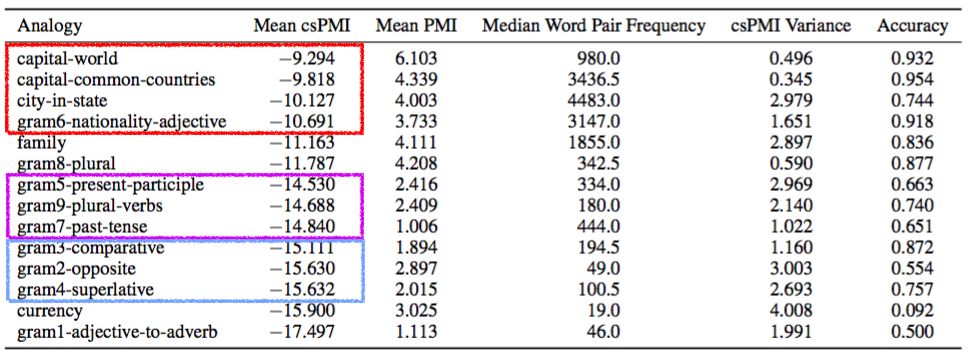
In the table above, we can see that
-
When the variance in csPMI is lower, solutions to analogies are more accurate (Pearson’s $r = -0.70$). This is because an analogy is more likely to hold over a set of word pairs when the geometric translations are identical, and thus when the csPMI values are identical.
-
Similar analogies, such as capital-world and capital-common-countries, have similar mean csPMI values. Our theory implies this, since similar analogies have similar translation vectors.
-
The change in mean csPMI mirrors a change in the type of analogy, from geography (red) to verb tense (purple) to adjectives (blue). The only outlier, currency, has a very high csPMI variance, very low accuracy, and word pairs that rarely co-occur in Wikipedia. Also note that while analogies correspond neatly to the mean csPMI, they have no relation to the mean PMI.
Euclidean Distance and csPMI
To test the interpretation of Euclidean distance offered by the csPMI Theorem, we plot $-\text{csPMI}(x,y)$ against $\|\vec{x} - \vec{y}\|^2$ for SGNS vectors trained on Wikipedia:
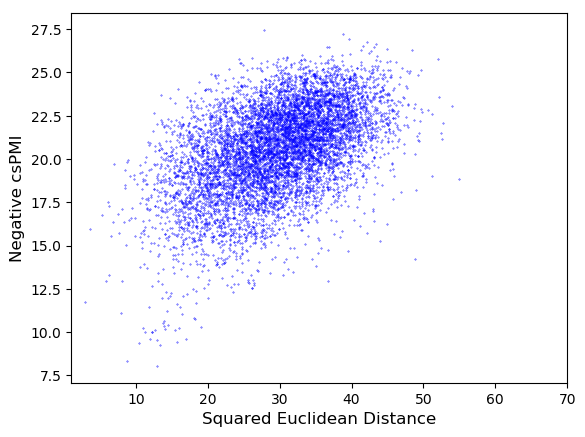
As expected, there is a moderately strong positive correlation (Pearson’s $r = 0.502$); the more similar two words are (as defined by csPMI), the smaller the Euclidean distance between their vectors. In the normalized word space, the correlation is just as strong (Pearson’s $r = 0.514$).
Conclusion
In a noiseless SGNS or GloVe space, a linear analogy holds exactly over a set of word pairs iff the co-occurrence shifted PMI is the same for every word pair and across any two word pairs, provided the row vectors of those words in the factorized word-context matrix are coplanar.
This, in turn, reaffirms the long-standing intuition on why word analogies hold, helps explain why vector addition is a decent means of composing words, and provides a new interpretation of Euclidean distance in word vector spaces. Unlike past theories of word analogy arithmetic, there is plenty of empirical evidence to support the csPMI Theorem, making it much more tenable.
If you found this post useful, you can cite our paper as follows:
@inproceedings{ethayarajh-etal-2019-towards,
title = "Towards Understanding Linear Word Analogies",
author = "Ethayarajh, Kawin and Duvenaud, David and Hirst, Graeme",
booktitle = "Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics",
month = jul, year = "2019", address = "Florence, Italy",
publisher = "Association for Computational Linguistics",
url = "https://www.aclweb.org/anthology/P19-1315",
doi = "10.18653/v1/P19-1315",
pages = "3253--3262",
}
Acknowledgements
Many thanks to Omer Levy and Yoav Goldberg for their helpful comments on an early draft of this paper, as well as the anonymous ACL reviewers. Special thanks to Graeme Hirst, Krishnapriya Vishnubhotla, Chloe Pou-Prom, and Allen Nie for their comments on this blog post. Thanks to Scott H. Hawley for catching a typo in the csPMI Theorem.
Footnotes
-
Gittens et al. (2017) criticized the latent variable model for assuming that word vectors are known a priori and generated by randomly scaling vectors sampled from the unit sphere. ↩
-
The original paraphrase model by Gittens et al. hinges on words having a uniform distribution rather than the typical Zipf distribution, which the authors themselves acknowledge is unrealistic. The revised model by Allen and Hospedales (2019) makes a highly unorthodox assumption that the negative sampling term in SGNS’ factorization is detrimental and can therefore be discarded. For any practical choice of $k$, which denotes the number of negative samples, the error term in Corollary 1.4 of that paper would be too large to explain the existence of word analogies. ↩
-
We do not need to worry about word vectors forming an anti-parallelogram that satisfies these conditions, as that would require the same direction in embedding space to correspond to two opposite relations (e.g., male → female and female → male), which is contradictory. ↩
-
Some previous work (Schluter, 2018; Rogers et al., 2017) has argued that word analogies should not be used for evaluating word embeddings, for a number of different theoretical and empirical reasons. This finding supports that idea: given that there are sensible analogies that do not satisfy the conditions in the csPMI Theorem, we should not treat the ability to solve analogies arithmetically as a perfect proxy for embedding quality. ↩